
SQUID GAME: Η ΦΥΣΙΚΗ ΠΙΣΩ ΑΠΟ ΤΟ ΠΑΙΧΝΙΔΙ ΤΗΣ ΔΙΕΛΚΥΣΤΙΝΔΑΣ
Squid game. Ο τρίτος γύρος ξεκινάει και ανακοινώνεται στους παίκτες ότι θα αγωνιστούν στην διελκυστίνδα. Η κάθε ομάδα θα αποτελείται από 10 άτομα. Οι δύο ομάδες θα τραβούν ένα σκοινί με σκοπό η μία να τραβήξει την άλλη προς το μέρος της. Πάμε να δούμε την φυσική που κρύβεται πίσω από το παιχνίδι αυτό!
Αν πριν από την έναρξη ενός αγώνα σας ζητούσα να ποντάρετε στην ομάδα που πιστεύετε ότι θα νικήσει ποια θα επιλέγατε; Υποθέτω την ομάδα που θα αποτελούνταν από τους πιο δυνατούς παίκτες, θεωρώντας πως όσο πιο δυνατοί είναι οι παίκτες μιας ομάδας τόσο πιο εύκολα θα μπορούσε να παρασύρει τους αντιπάλους της. Και μάλλον σε αυτή την περίπτωση το στοίχημα μας θα πήγαινε κουβά. Η διελκυστίνδα δεν είναι παιχνίδι δύναμης αλλά τρίβης. Πάμε να ξεκινήσουμε με την ανάλυση!
Tι θα διαβάσετε σε αυτό το άρθρο:
ΔΥΝΑΜΕΙΣ ΕΠΑΦΗΣ-ΔΡΑΣΗ ΑΝΤΙΔΡΑΣΗ-3Ος ΝΟΜΟΣ ΝΕΥΤΩΝΑ
Πριν περάσουμε όμως στην διελκυστίνδα ας ξεκινήσουμε με ένα απλό παράδειγμα ώστε να κατανοήσουμε λίγο τις δυνάμεις επαφής, την έννοια δράσης-αντίδρασης και τον τρίτο νόμο του Νεύτωνα. Έστω ότι έχουμε ένα κιβώτιο όπως φαίνεται στο σχήμα 1 σε λείο δάπεδο, το οποίο ηρεμεί και στο σώμα αυτό έχουμε δεμένο ένα αβαρές νήμα.

Το άλλο άκρο το κρατάμε εμείς και ασκούμε μία δύναμη f1. Ας δούμε τις δυνάμεις που εμφανίζονται. Το σκοινί βρίσκεται σε επαφή με το χέρι μας και με το κουτί άρα δέχεται την δύναμη f1 από το χέρι μας και την δύναμη f2 από το κουτί. (δυνάμεις επαφής). Δυνάμεις επαφής είναι οι δυνάμεις που ασκεί ένα σώμα σε ένα άλλο όταν βρίσκονται σε επαφή και αλληλεπιδρούν. Στην περίπτωση που θεωρήσουμε το νήμα αβαρές προκύπτει από τον δεύτερο νόμο του Νεύτωνα ότι f1 = f2!
Το σχοινί τώρα θα ασκεί μία δύναμη Τ1 στο χέρι μας ίσου μέτρου με την f1, όπως φαίνεται στο σχήμα 2 , διότι η Τ1 είναι η αντίδραση της f1.
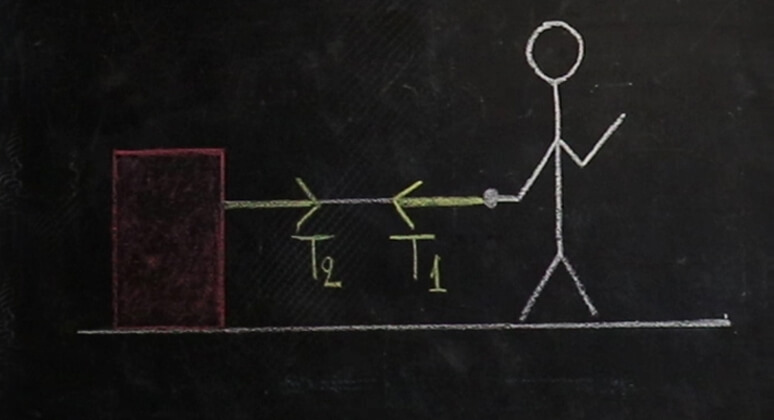
Και η δύναμη Τ2 θα είναι ίση με την f2 ως αντίδραση της. Άρα αφού f1 = f2 θα έχουμε και Τ1 = Τ2. Συνεπώς, αν σκεφτούμε τώρα το παιχνίδι της διελκυστίνδας βλέπουμε πώς αν αυξήσω την δύναμη που τραβάω, η δύναμη αυξάνεται και από την άλλη μεριά, και μάλλον αρχίζουμε να καταλαβαίνουμε πως δεν θα κερδίσει ο πιο δυνατός.
ΑΝΑΛΥΣΗ ΔΥΝΑΜΕΩΝ ΣΤΗΝ ΔΙΕΛΚΥΣΤΙΝΔΑ
Ας περάσουμε τώρα στο παιχνίδι της διελκυστίνδας και στην ανάλυση των δυνάμεων ώστε να δούμε ποιες δυνάμεις ασκούνται πάνω στον παίκτη της κάθε ομάδας.
Η κίνηση που μας αφορά βρίσκεται στον άξονα χ΄χ. Και εφόσον οι δυνάμεις που τραβάμε ο ένας τον άλλον είναι ίσες όπως αποδείξαμε προηγουμένως, το παιχνίδι θα καθοριστεί από τις τριβές.
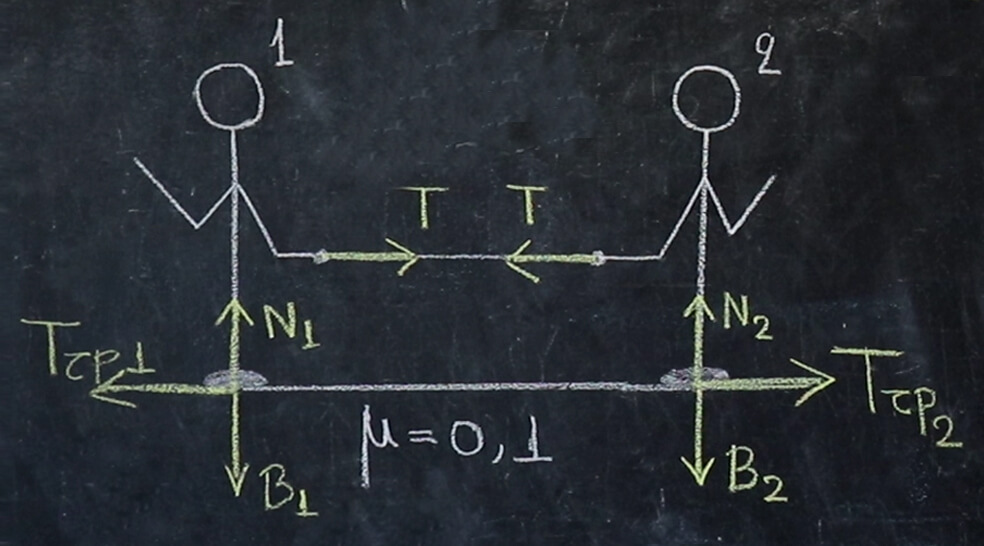
ΤΡΙΒΗ-ΣΤΑΤΙΚΗ ΤΡΙΒΗ-ΤΡΙΒΗ ΟΛΙΣΘΗΣΗΣ
Η τριβή είναι η δύναμη που εκδηλώνεται μεταξύ δύο σωμάτων όταν το ένα κινείται έναντι του άλλου ή τείνει να κινηθεί. Ο τύπος για τον υπολογισμό της τριβής είναι Τ = μΝ. Στην περίπτωσή μας, αφού τα σώματα ισορροπούν στον άξονα ψ΄ψ εύκολα από τον πρώτο νόμο του Νεύτωνα συμπεραίνει κανείς πως το Ν είναι ίσο με το βάρος. Άρα λοιπόν βλέπουμε πώς η τριβή αυξάνεται ή μειώνεται ανάλογα με τον συντελεστή τριβής και την μάζα του αντικειμένου. Ας υποθέσουμε πως και οι δύο παίκτες φοράνε τα ίδια παπούτσια άρα έχουν ίδιο συντελεστή τριβής (μ=0,1) αλλά η μάζα του πρώτου είναι 100 κιλά ενώ η μάζα του δεύτερου 60 κιλά. Με υπολογισμούς μπορεί να βρει κανείς πώς η τριβή που εμφανίζεται στον πρώτου παίκτη είναι 100Ν και η τριβή που εμφανίζεται στον δεύτερο παίκτη 60Ν. Αν αρχικά ο παίκτης νούμερο ένα τραβάει το σκοινί με δύναμη 50 newton κανείς δεν θα μετακινηθεί διότι και στους δύο παίκτες οι τριβές είναι μεγαλύτερες από τις δυνάμεις που θέλουν να τους μετακινήσουν. Αν όμως ο παίκτης ένα αποφασίσει να βάλει περισσότερη δύναμη π.χ. 80Ν τότε η δύναμη αυτή θα είναι ίση και από την άλλη μεριά. Άρα ο παίκτης δύο θα μετακινηθεί προς τα αριστερά διότι η τάση του νήματος, η δύναμη δηλαδή που τον τραβάει προς τα αριστερά θα γίνει μεγαλύτερη από την τριβή που αναπτύσσεται πάνω του.
ΚΕΝΤΡΟ ΒΑΡΟΥΣ-ΡΟΠΗ ΔΥΝΑΜΗΣ
Πάμε τώρα να εξετάσουμε και μία ακόμα λεπτομέρεια. Αν έχετε προσέξει οι παίκτες κατά την διάρκεια του αγώνα κάθονται ελαφρώς, προσπαθώντας να χαμηλώσουν το κέντρο βάρους τους. Γιατί όμως αυτό είναι σημαντικό; Εδώ έρχεται ο ρόλος της ροπής μιας δύναμης. Ροπή, είναι η ικανότητα που έχει μία δύναμη στο να περιστρέψει ένα σώμα και ο μαθηματικός τύπος για τον υπολογισμό της είναι τ=F*R όπου F είναι η δύναμη που ασκείται και R είναι η απόσταση από τον άξονα περιστροφής και το σημείο όπου ασκείται η δύναμη. Αν κοιτάξουμε τον τύπο μπορούμε εύκολα να καταλάβουμε πως η ροπή μπορεί να μεγαλώσει ή αν αυξήσω την δύναμη ή αν ασκήσω την δύναμη πιο μακριά από τον άξονα περιστροφής του σώματος. Για να το κατανοήσουμε ας σκεφτούμε ένα απλό καθημερινό παράδειγμα. Για να ανοίξετε μία πόρτα, που ασκείται την δύναμη; Κοντά στο πόμολο ή κοντά στον μεντεσέ, που βρίσκεται στον άξονα περιστροφής της; Φυσικά στο πόμολο, διότι είναι το σημείο με τη μεγαλύτερη απόσταση από τον άξονα περιστροφής της και κατά αυτό τον τρόπο η ροπή μεγαλώνει, δηλαδή η ικανότητα να περιστρέψουμε την πόρτα. Στην περίπτωση της διελκυστίνδας αν αρχικά είμαστε όρθιοι τότε η ροπή θα είναι μεγαλύτερη από ότι αν καθόμασταν ελαφρώς και ο λόγος είναι ότι στην περίπτωση που είμαστε όρθιοι η απόσταση που ασκείται η δύναμη από τον άξονα περιστροφής είναι μεγαλύτερη από την δεύτερη περίπτωση. Οπότε λοιπόν στην περίπτωση που βρισκόμαστε όρθιοι είναι ευκολότερο να ανατρέπουμε.
Οπότε αν κληθείτε να παίξετε ποτέ αυτό το παιχνίδι, φροντίστε η ομάδα σας να φοράει καλά παπούτσια και να έχει άτομα που τρώνε όλο το φαγητό τους και θα αποτελείται από άτομα που δεν καμαρώνουν για το ύψος τους!
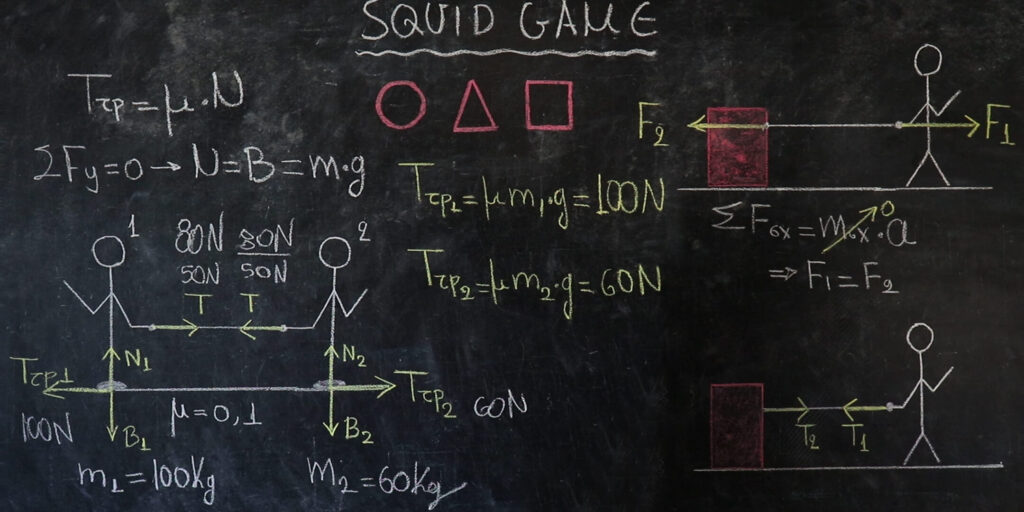
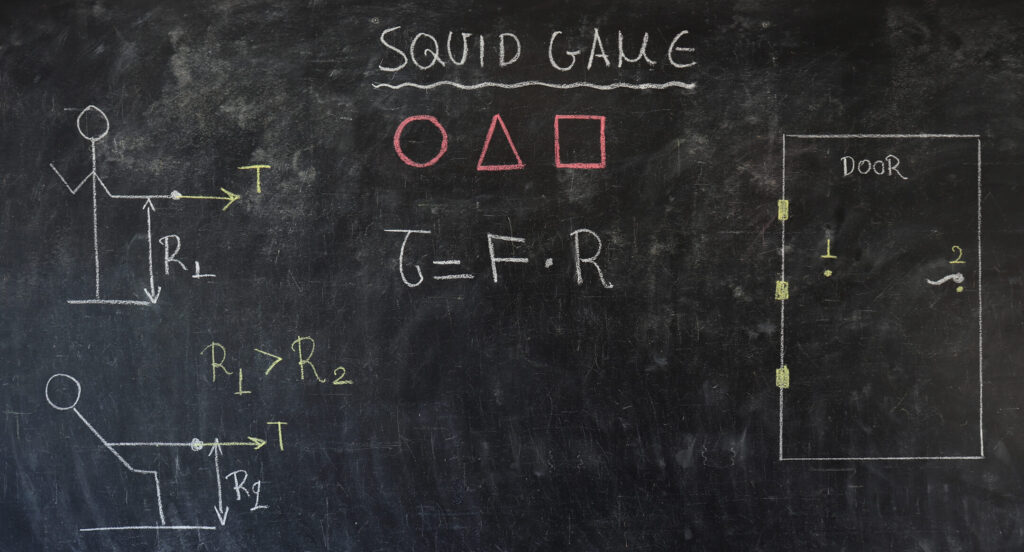
Tag:fainomena


