
ΠΕΙΡΑΜΑΤΑ ΜΕ ΤΗΝ ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ ΚΥΛΙΝΔΡΟΥ ΔΑΚΤΥΛΙΟΥ ΚΑΙ ΡΑΒΔΟΥ
Στη συγκεκριμένη παρουσίαση θα παρακολουθήσουμε πειράματα που αφορούν την ροπή αδράνειας και τον ρόλο που αυτή θα παίξει κατά την περιστροφική κίνηση των αντικειμένων. Πριν όμως περάσουμε στα πειράματα μας να δούμε λίγο τι είναι ροπή αδράνειας ώστε να κατανοήσουμε καλύτερα την επεξήγηση των αποτελεσμάτων των πειραμάτων μας. Και για να καταλάβουμε καλύτερα την ροπή αδράνειας ας κάνουμε ένα flashback στην αδράνεια των σωμάτων κατά την μεταφορική τους κίνηση.
Tι θα διαβάσετε σε αυτό το άρθρο:
ΤΙ ΕΙΝΑΙ Η ΑΔΡΑΝΕΙΑ;
Αδράνεια είναι η ιδιότητα των σωμάτων να αντιστέκονται σε οποιαδήποτε μεταβολή της κινητικής τους κατάστασης. Όταν ασκώ μια δύναμη πάνω σε ένα αντικείμενο τότε αυτό θέλει να αντισταθεί στην μεταβολή της κινητικής του κατάστασης που προσπαθω να του επιφέρω. Και το μέτρο της αδράνειας είναι η μάζα. Όσο μεγαλύτερη είναι η μάζα ενός αντικειμένου τόσο πιο δύσκολα θα μπορέσω εγώ να το θέσω σε κίνηση από την ακινησία.
ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ
Αντίστοιχα τώρα αν είχαμε έναν κύλινδρο και του άκουσα μία δύναμη στην περιφέρεια του αυτή η δύναμη προκαλεί ροπή, δηλαδή θέλει να περιστρέψει το αντικείμενο. Όσο μεγαλύτερη είναι η ροπή αδράνειας όμως του αντικειμένου τόσο πιο δύσκολα θα ξεκινήσει την περιστροφή. Για τον υπολογισμό ροπής αδράνειας χρησιμοποιήσουμε ένα έτοιμο τυπολόγιο το οποίο μπορείτε να δείτε στον από κάτω πίνακα. Πάμε λοιπόν να ξεκινήσουμε με τα πειράματά μας!
1ο ΠΕΙΡΑΜΑ:
Για να εξηγήσουμε το πρώτο μας πείραμα θα κάνουμε μία ενεργειακή προσέγγιση. Οι ενέργεις που μας αφορούν στο συγκεκριμένο πρόβλημα είναι η δυναμική η οποία εξαρτάται από το ύψος του αντικειμένου και η κινητική η οποία εξαρτάται από την ταχύτητά τους. Τα δύο σώματα αρχικά τα αφήσαμε να κινηθούν από το ίδιο ύψος έχοντας αρχική ταχύτητα 0. Οπότε αντιλαμβανόμαστε ότι και τα δύο σώματα αρχικά έχουν την ίδια ενέργεια. Και καθώς κινούνται προς τη βάση η δυναμική ενέργεια αυτή θα μετασχηματιστεί σε κινητική. Όμως η κινητική των σωμάτων δεν είναι μόνο μεταφορική. Οι ταχύτητες που αποκτούν τα αντικείμενα είναι η μεταφορική που μας δείχνει το πόσο γρήγορα μεταφέρεται το σώμα και περιστροφική μας δείχνει πόσο γρήγορα περιστρέφεται. Αρα η κινητική ενέργεια θα έχει δύο μορφές την κινητική μεταφορική και την κινητική στροφική.
Και σύμφωνα με την απόδειξη που έχουμε γράψει το αντικείμενο που θα έχει την μικρότερη ροπή αδράνειας θα πάρει το μικρότερο ποσό από την αρχική δυναμική ενέργεια και θα τη μετατρέψει σε κινητική περιστροφική οπότε το μεγαλύτερο ποσό ενέργειας θα μεταφερθεί στην κινητική μεταφορική κάνοντας έτσι την ταχύτητα κέντρου μάζας του κυλίνδρου μεγαλύτερη από την ταχύτητα κέντρου μάζας του δακτυλίου καθιστώντας τον έτσι νικητή του αγώνα!
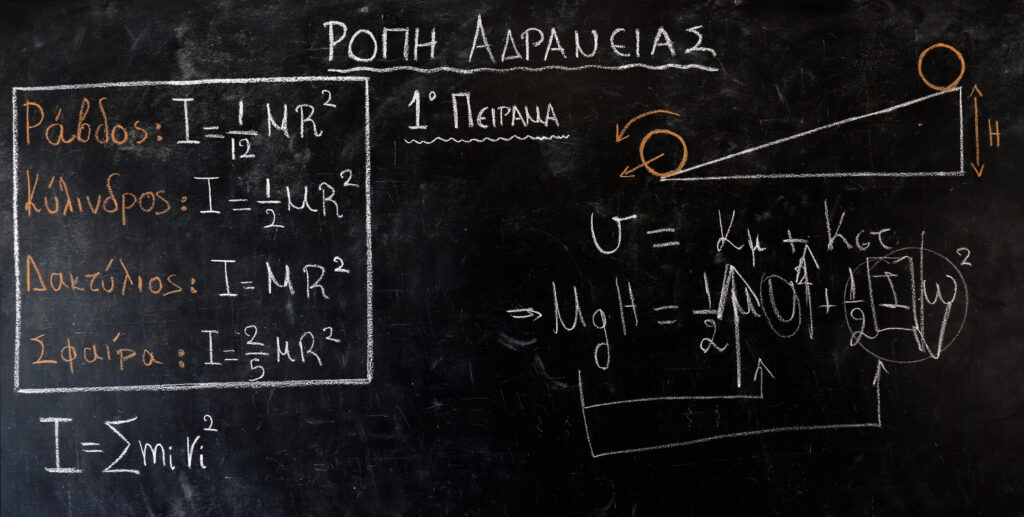
2ο ΠΕΙΡΑΜΑ:
Στο δεύτερο πείραμα οι διαγωνιζόμενοι ήταν μία σφαίρα και ένας κύλινδρος! Και το σημαντικό σε αυτή την περίπτωση ήταν ότι ήταν διαφορετικής μάζας, η μάζα του κυλίνδρου ήταν πολύ μεγαλύτερη από τη μάζα της σφαίρας. Άρα λοιπόν αρχικά θα περίμενε κάποιος το αντικείμενο με τη μεγαλύτερη μάζα να κινηθεί ταχύτερα και να φτάσει πρώτος στη βάση του κεκλιμένου επιπέδου. Όμως συνέβη ακριβώς το αντίθετο. Ο λόγος λοιπόν φαίνεται στην παρακάτω απόδειξη και είναι πως ο συντελεστής που ορίσαμε μπροστά από το MR^2 στην κάθε ροπή μας υποδεικνύει τον τρόπο που είναι κατανεμημένη η μάζα. Όσο μικρότερος είναι αυτός ο συντελεστής τόσο μεγαλύτερη θα είναι η ταχύτητα κέντρου μάζας που θα αποκτήσει το αντικείμενο καθιστώντας έτσι στη συγκεκριμένη περίπτωση νικήτρια του αγώνα την σφαίρα!
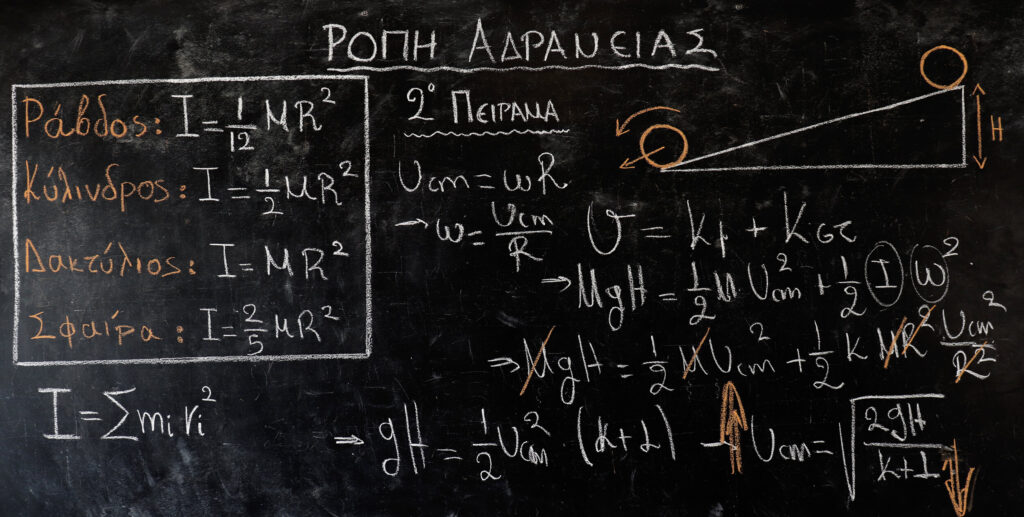
3ο ΠΕΙΡΑΜΑ:
Στο τρίτο μας πείραμα οι διαγωνιζόμενοι ήταν μία ράβδος και μία όμοια ράβδο με την πρώτη μόνο που είχαμε τοποθετήσει στο άκρο της μία μάζα, τη μάζα μιας πατάτας! Στην περίπτωση αυτή όπως θα δείτε και στην παρακάτω απόδειξη υπολογίσαμε την ροπή αδράνειας μιας ράβδου ως προς άξονα περιστροφής στο άκρο της και έπειτα υπολογίσαμε την ροπή αδράνειας του συστήματος ράβδου πατάτας με άξονα περιστροφής και πάλι το άκρο της. Αυτό που παρατηρούμε είναι πως η ροπή αδράνειας του συστήματος ράβδου πατάτας είναι μεγαλύτερη από την ροπή αδράνειας μόνο της ράβδου πράγμα το οποίο σημαίνει πως όσο μεγαλύτερη είναι η ροπή αδράνειας τόσο δυσκολότερα θα ξεκινήσει η περιστροφική κίνηση του αντικειμένου. Καθιστώντας έτσι η νικήτρια την ράβδο η οποία δεν είχε μία μάζα στο άκρο της.
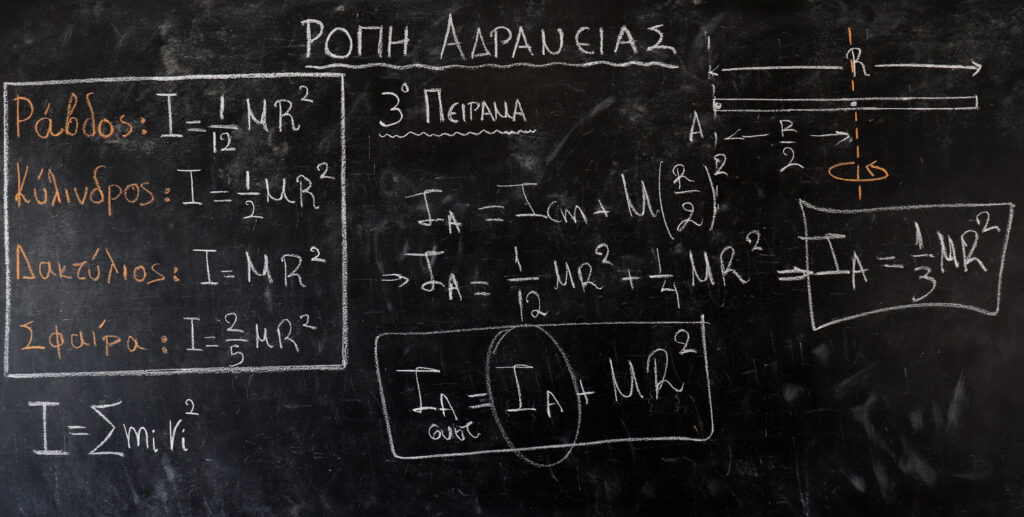
Tag:peirama


