Η ΔΙΑΣΤΟΛΗ ΤΟΥ ΧΡΟΝΟΥ ΚΑΙ Η ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ ΤΟY ALBERT EINSTEIN

Χρόνος… Δεν τον βλέπουμε, δεν τον ακούμε μα τον βιώνουμε κάθε στιγμή. Είναι όμως ο χρόνος ίδιος για όλους; Για να δώσουμε απάντηση στο ερώτημά αυτό θα πρέπει να μεταφερθούμε πίσω στο χρόνο και να πάμε κάπου στις αρχές του 1900 όπου ο νεαρός Αlbert Εinstein διατύπωσε την ειδική θεωρία της σχετικότητας.

ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ

Για να κατανοήσουμε καλύτερα τα όσα θα πούμε σε λίγο θα πρέπει να κάνουμε μία μικρή αναφορά αρχικά στην σχετικότητα των κινήσεων και τι καλύτερο από ένα παράδειγμα. Θέλω να
φανταστείτε τον εαυτό σας μέσα σε ένα αυτοκίνητο το οποίο κινείται με ταχύτητα 100  χιλιομέτρων ανά ώρα και στα χέρια σας κρατάτε ένα φρέντο εσπρέσσο. Αν κοιτάξετε τον καφέ σας και σας ρωτήσω είναι ακίνητος η κινείται, τότε απλά θα τον κοιτάξετε και θα μου πείτε πώς τον βλέπετε ακίνητο. Και η απάντησή σας θα είναι σωστή! Αν όμως ρωτούσατε εμένα που κάθομαι στην άκρη του δρόμου και σας παρακολουθώ, θα έβλεπα τον καφέ σας να κινείται με ταχύτητα 100 χιλιομέτρων ανά ώρα. Έτσι λοιπόν διαπιστώνουμε τη σχετικότητα των κινήσεων σύμφωνα με ένα σύστημα αναφοράς.

ΑΞΙΩΜΑΤΑ ΕΙΔΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ

Ο Αlbert Εinstein στην ειδική θεωρία της σχετικότητας έθεσε δύο αξιώματα. Σύμφωνα με το πρώτο οι νόμοι της φύσης είναι ίδιοι σε όλα τα αδρανειακά συστήματα και το δεύτερο είναι πως η ταχύτητα του φωτός είναι ίδια σε όλα τα αδρανειακά συστήματα. Το αξίωμα με την ταχύτητα του φωτός μας ενδιαφέρει ιδιαίτερα στην απόδειξη που θα ακολουθήσει στο τέλος μιας και θα παίξει καθοριστικό ρόλο. Στην κουβέντα μας μπλέξαμε παρατηρητές, χρόνο, φως…

Οπότε ας τα βάλουμε όλα μαζί μέσα σε ένα βαγόνι να δούμε τι θα γίνει. Πριν μπούμε όμως μέσα στο βαγόνι να αναφερθούμε πως τα μαθηματικά που θα χρησιμοποιήσουμε θα είναι αρκετά απλά
και πιο συγκεκριμένα θα χρειαστούμε ένα Πυθαγόρειο θεώρημα και τον τύπο που μας δίνει την απόσταση σε μία ευθύγραμμη ομαλή κίνηση, όταν δηλαδή η ταχύτητα που κινείται ένα σώμα είναι σταθερή. Αν κοιτάξετε τον πίνακα που παραθέτω παρακάτω θα δείτε την απόδειξη και ένα σχήμα. Στο σχήμα μπορείτε να δείτε έναν παρατηρητή Α και έναν παρατηρητή Β. Ο παρατηρητής Α βρίσκεται ακίνητος εκτός του βαγονιού και ο παρατηρητής Β βρίσκεται ακίνητος εντός του βαγονιού. Η άσπρη κιμωλία συμβολίζει την κίνηση του φωτός που θα ξεκινήσει από την άκρη του φακού που κρατάει ο παρατηρητής Β και θα κινηθεί προς το άνω άκρο του βαγονιού. Αυτό που θα συμβεί είναι πως το βαγόνι θα κινείται με μία σταθερή ταχύτητα και θα απομακρύνεται από τον παρατηρητή Α. Οπότε το θέμα είναι ποια είναι η απόσταση που βλέπει ο παρατηρητής Β που διανύει το φως και ποια είναι η απόσταση που βλέπει ο παρατηρητής Α ότι διανύει το φως. Αυτό
που τελικά προκύπτει είναι ένα ορθογώνιο τρίγωνο όπου και θα χρησιμοποιήσουμε το Πυθαγόρειο θεώρημα για να κάνουμε τη συσχέτιση των δύο χρόνων, του χρόνου δηλαδή που καταγράφει ο παρατηρητής Α σε σχέση με τον χρόνο που καταγράφει ο παρατηρητής Β.

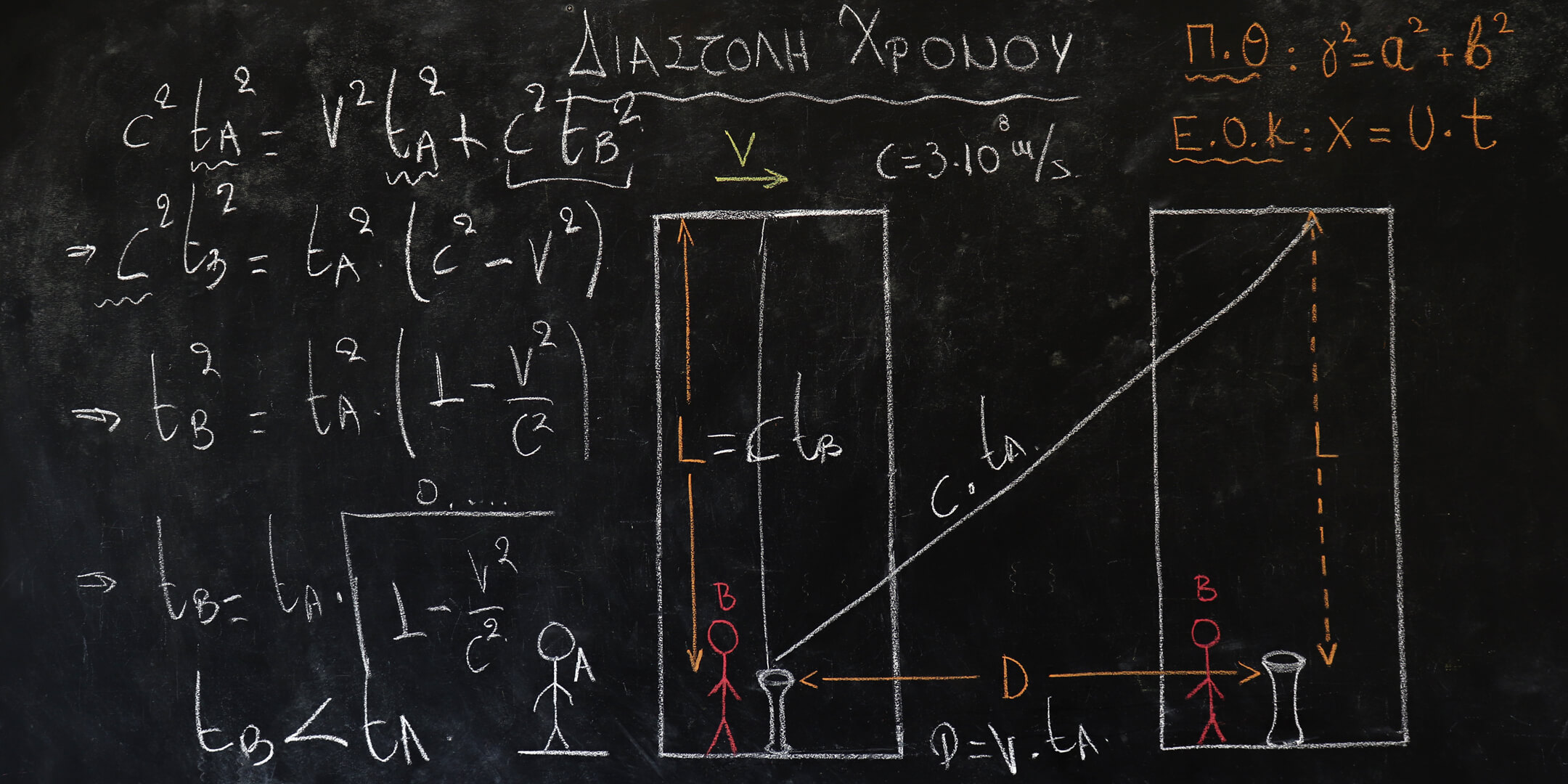
Αν κοιτάξουμε την κατάληξη της απόδειξης προκύπτει πως ο χρόνος ως προς τον παρατηρητή Α κυλάει πολύ πιο αργά σε σχέση με τον χρόνο που καταγράφει ο παρατηρητής Β. Αυτό σημαίνει με ένα απλό παράδειγμα πως αν για τον παρατηρητή Α περάσανε 10 χρόνια τότε για τον παρατηρητή Β θα έχουν περάσει μόνο δύο χρόνια. Αυτή λοιπόν ήταν η ερμηνεία της διαστολής του χρόνου σύμφωνα με την ειδική θεωρία της σχετικότητας του Albert Einstein.